Ryerson Computer Science CPS721: Artificial Intelligence
(go back)Gottfried Leibniz
- "Thinking can be usefully understood as a computational process"
- rules of arithmetic can be used to deal with abstract numbers symbolically
- thus, similarly rules of logic can be used to deal with abstract ideas symbolically as well
Knowledge Base Techniques
Back-chaining
- Chains backward from the query to the atomic sentences in the KB
Back-tracking
- When a failure is found in one path of the chain, but another path may be tested. Back-tracks back up and down another branch
Prolog
Basic Syntax
- constants: must start with lower case
- variables: must start with upper case or underscore
- predicate definition: predicate(arg1,arg2,arg3)
- conditional statements: predicate(args) :- anotherPredicate(args).
- boy(Name) :- male(Name), young(Name).
- term: like a data structure, can be used as an argument to a predicate
Lists
- Equal if: same number of elements in same positions
- Vertical Bar notation: v-bar can be inserted between elements; the elements that follow the bar become elements of a new list. Eg:
- [ a, b, c ] == [ a | [ b, c ] ]
- the opposition operation can be done too -> remove a bar, merge the following list's elements into the current list
- General Rules:
- X can match anything -- a single value element, or a list of elements (but NOT free-form elements not contained in a list)
- [ X ] matches only a list with 1 element (that 1 element could be another list, remember!)
- [ X | Y ] matches only a list with 1 or more elements
- [ X , Y ] matches only a list with 2 elements
Arithmetic
Arithmetic expressions made up of variables, integers, parentheses, and these operators:
- +
- -
- *
- // (integer division)
- / (regular decimal dividions)
- mod
- ^
Comparison
Predicates for comparison: <, =<, >, >=
Predicate for equality of arith expression: =:=
Assignment (is)
Usage: variable is arith_expression
- if variable is unassigned, assigns result of arith expression to the variable
- else, if variable is assigned, tests for equality between variable value and expression like =:=
Common Functions
- member(X,List). // indicates if X is a member of List
- sum(+X, +Y, -Z). // indicates X,Y must be provided as inputs, Z is output
Command-Line
- go to /sw1/Eclipse/bin/i386_linux/eclipse
- run: ./eclipse -b yourfilename.pl
Recursion
General Procedure:
- Consider the Head and Tail of the list
- Process the Head
- Recursively Process the Tail
Hints:
- In developing a recursive function, step through several iterations of successive values until a general pattern can be spotted
Example functions developed in class (see notes 04):
- member( X, List ).
member( Head, [ Head | Tail ] ).member( Head1, [ Head2 | Tail ] ) :- not Head1 = Head2, member( Head1, Tail ).
- append( List1, List2, ResultList ).
append( [ ], List2, List2 ).append( [ X | List1 ], List2, [ X | Result ] ) :- append( List1, List2, Result ).
- sum( ListOfNumericElements, Sum ).
sum( [ ], 0 ).sum( [ Head | Tail ], S ) :- sum ( Tail, Q ), S is Q + Head.
- length( List, LengthOfList ).
length( [ ], 0 ).length( [ Head | Tail ], N ) :- length( Tail, M ), N is M + 1.
- writeList( List ).
writeList( [ ] ).writeList( [ X | Tail ] ) :- write(X), nl, writeList(Tail).
- reverseWriteList( List ).
reverseWriteList( [ ] ).reverseWriteList( [ X | Tail ] ) :- reverseWriteList(Tail), nl, write(X).
Constraint Satisfaction Problems
examples:
- map colouring
Example: using "Generate & Test" pattern
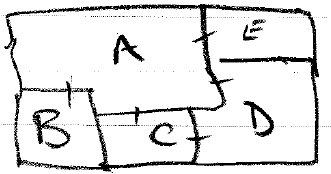 Constraints: 5 countries: A, B, C, D, E; 3 colours: red, blue, white
Constraints: 5 countries: A, B, C, D, E; 3 colours: red, blue, white
/* define the colours */colour(red).colour(blue).colour(white).
/* solve; first Generate (values) */solve( [ A, B, C, D, E ] ) :- colour(A), colour(B), colour(C),colour(D), colour(E),colour(D), colour(E),
/* then Test (constraints) */not A = B, not A = C, not A = E, not A = D,not B = C, not C = D, not E = D.
Note that this uses the simple Generate and Test approach which is highly inefficient. Prolog will generate all the values for A through E first, before testing any constraints. Prolog will assign all the same values the first time, then change the last variable through all combinations of possible values, before moving to the second last variable, etc. This results in many 'fails', which means a lot of back-tracking, and thus very slow to find any solution, if one exists. For best performance, interleave Tests with Generated values. Must always generate values though, even if they are known - crypt-arithmetic problem solving
SEND+ MORE-----MONEY
- scheduling
Pattern for solving:
- identify the domain values
- choose a predicate (usually one, sometimes two) to generate values for variables
- choose variables that will be set with the values of the particular domain
- define the domain with actual constants via the predicate
- implement the constraints one at a time; generate variable values just before testing for most efficient program
- implement additional helper predicates as needed
- may choose an optimal order for generating values by creating a dependency graph (start with the most 'independent')
Natural Language Understanding
Linguistics
- Morphology: roots of words, prefixes, suffixes
- Syntax: how are the words grouped
- Semantics: what do the words mean?
- Pragmatics: what are the words being used for?
Lexicon
- Word categories of the language, and the vocabulary in each category
- Articles: a, the
- Adjectives: fat, fich, happy...
- Proper nouns: Mary, John, Toronto
- Common nouns: boy, sweater, milk
- Transitive verbs: kick, love, throw
- Intransitive verbs: walk, sleep, die, listen
- Copula verbs: be, seem, ...
- Prepositions: in, on, from, beside, ...
- Others (pronouns, adverbs, interjections)
Grammar
- lexical (terminal) categories, like an article or transitive verb; written in lower case
- group (non-terminal) categories, like a phrase or a sentence; written in upper case
- grammar for declarative sentences (CLICK HERE)
S -> NP VPVP -> copula_verb ModsVP -> transitive_verb NP ModsVP -> intransitive_verb ModsMods -> []Mods -> PP ModsPP -> preposition NPNP -> proper_nounNP -> article NP2NP2 -> adjective NP2NP2 -> common_noun Mods
General Problem Solving
- Basic idea: we have states, and we have operators that can cause transitions between states.
- Basic problem solving code:
reachable( S, [ ] ) :- initial_state(S).reachable( S, [ M | L ] ) :- reachable(S, L), legal_move(S, M, S2).solve_problem(L) :- reachable(S, L), goal_state(S).