Ryerson Computer Science CPS615: Theory of Parsing
(go back)Deterministic Finite Automata (DFA)
A = (Q, $\Sigma$, $\delta$, q$_0$, F)
- Q is finite states
- $\Sigma$ is finite alphabet
- $\delta$ is transition function, eg $\delta$(q$_0$, 1) -> q$_1$
- q$_0$ $\in$ Q is the start state
- F $\subset$ (or equal) Q is the set of (possibly multiple) final states
Extended Transition Function
$\hat\delta$(q$_0$, w) returns the final state after w has been processed if the starting state is q$_0$
Language of a DFA
L(A) = {w | $\hat\delta$(q$_0$, w) is in F}
This means that the language of a given deterministic Finite Automaton is given by all the words in the language
Transition Table Notation
A matrix of values which are the destination state after the transition. The first row (header row) is the transition symbol, the first column is the current state.
Non-deterministic Finite Automata (NFA)
Obtain DFA from NFA
Two approaches:
- "naive" subset construction method (uses all combinations of states)
- "lazy" subset construction method (uses only the combinations of states that are transitioned to from the initial state)
$\epsilon$-NFA
contains some $\epsilon$ transitions that allow transition to the next state without consuming any input symbol
ECLOSE
ECLOSE(q) returns the set of states that can be travelled to from q via $\epsilon$'s. Always includes q even if there is no $\epsilon$.
$\epsilon$-NFA to DFA
note about transition states: the procedure dictates that you must find the destination states after the transition, AND the ECLOSE of that set of states. Need an example here
Regular Expressions
Kleen Closure
$L^* = \bigcup_{i = 0}^{\infty}L^i$
- this always includes $\epsilon$ in the set since $L^0$ is {$\epsilon$}
Language Properties
suppose E, F are regular expressions
- L((E)) = L(E)
- Eg, L(01) = {01}
- L(E + F) = L(E) + L(F) [or condition]
- Eg, L(01 + 0) = {01,0}
- L(E$\cdot$ F) = L(E) $\cdot$ L(F)
- Eg, L(0(1+0)) = {01, 00}
- L(E*) = (L(E))*
-
L(0*) = {$\epsilon$, 0, 00, 000, ..., $0^n$}
L((0 + 10)*) = $L^*$ + $L^1$ + $L^2$ + $L^3$ + ... + $L^n$
= {$\epsilon$} $\bigcup$ {0,10} $\bigcup$ {00, 010, 100, 1010} $\bigcup$ {000, 0010, 0100, 01010, 1000, 10010, 10100, 101010}
-
L(0*) = {$\epsilon$, 0, 00, 000, ..., $0^n$}
Regular Expressions Properties
- $(\epsilon + R)^* = R^*$
- $(\epsilon + R)R^* = R^*(\epsilon + R) = R^*$
- $R + RS^* = RS^*$
- $R + S^*R = S^*R$
- $\phi R = R\phi = \phi ~~(annihilation)$
- $\phi + R = R + \phi = R$
DFA to Regex: with recursive algorithm (long method)
Basis:
(For any action, a, defined by the transition table (or state diagram))
For a transition from a state to itself: $a + \epsilon$
For a transition from a state to another state: $a$
Induction:
$R_{ij}^{(k)} = R_{ij}^{(k-1)} ~+~~ R_{ik}^{(k-1)}(R_{kk}^{(k-1)^*})R_{kj}^{(k-1)}$
DFA to Regex: by state elimination
- Eliminate intermediate (non-beginning, non-final) states
- Eliminate multiple final states separately, then OR them all together
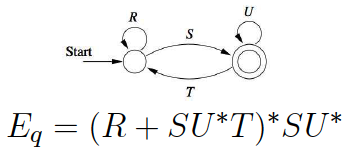
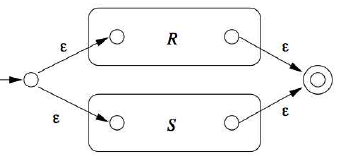
Regular Expression to $\epsilon$-NFA
Following is a list of symbolic components to be used in the process of converting regular expressions to $\epsilon$-NFA. Following this operation, one can convert from the $\epsilon$-NFA to DFA using the approach noted in an earlier section
- R* (kleen closure)
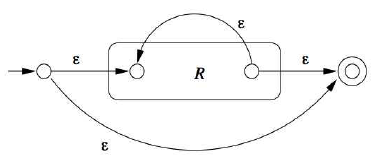
- RS (concatenation)
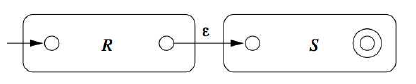
- R+S (disjunction)
Properties of Regular Languages
Algebraic Laws
- Union: commutative & associative
-
L + M = M + L
( L + M ) + N = L + ( M + N )
-
L + M = M + L
- Concatenation: associative (NOT commutative)
- L(MN) = (LM)N
- Distributive Law
-
L(M + N) = LM + LN
(M + N)L = ML + NL
-
L(M + N) = LM + LN
Regular Language Verification
Regular languages have at least 4 different descriptions that represent them:
- DFA
- NFA
- $\epsilon$-NFA
- Regular Expressions
The Pumping Lemma
Used to prove that a language is *not* regular (by contradiction). The pumping lemma states:
There exists $n$ s.t. for every string $w$ in L s.t. $\vert w \vert \ge n$ we can break $w$ into 3 strings, $w = xyz$, such that:
- $y \ne \epsilon$
- $\vert xy \vert \le n$
- $\forall k \ge 0,$ the string $xy^kz$ also is in L [this is the part that pumps]
Closure Properties of Regular Languages
Equivalence and Minimization of Automata
Table-filling Method for finding Equivalence
Basis: if p is an accepting state and q is a non-accepting state, then the pair {p, q} is distinguishable (not equivalent)
Induction: if the same input string reaches two (already known) distinguishable states, then the originating two states are distinguishable. Used in the "table filling method"
Minimizing
Steps:
- Transform into a DFA (using any method)
- Eliminate any states that cannot be reached from the start state (useless cruft)
- Use the table-filling method to find non-distinguishable states
- Partition those states into sets of indistinguishable states (sets of states that are distinguishable as per empty boxes in the table, and individual states that have all boxes filled with X's)
Context-Free Language Grammars
Larger class of languages (of which regular is a subset) called "context free". Consists of grammatical rules with the following basic components:
- set of terminal symbols
- set of variables (non-terminal)
- start symbol
- set of production rules that represent the recursive definition of the language
E $\rightarrow$ I
E $\rightarrow$ E + E
I $\rightarrow$ a
etc...
Representations: Left-Most Derivation, Right-Most Derviation, Parse Tree
Sentential Form
Ambiguous Grammar (pg 207)
In order to avoid ambiguous grammars, that are usually a result of precedence problems, introduce new variables:
- Factor: expression that cannot be broken apart by any adjacent operator, either a * or a+. Factors include identifiers, and any parenthesized expressions
- Term: expression that cannot be broken by + operator.
Example of unambiguous grammar:
- I $\rightarrow$ a | b | Ia | Ib | I0 | I1
- F $\rightarrow$ I | (E)
- T $\rightarrow$ F | T * F
- E $\rightarrow$ T | E + T
Pushdown Automata - machines to represent context-free languages
PDA's can represent context free grammars, and vice-versa
Diagram Transition Notation
A, B / C
- A is the input symbol
- B is the symbol that must reside at the top of the stack
- C is the symbol (or set of symbols) that replace B at the top of the stack
Example: 1, 1 / 10. If the input is 1, and 1 is at the top of the stack, then replace 1 with 10. In other words, push 0 onto the stack.
Example: 1, 0 / $\epsilon$. If the input is 1, and 0 is at the top of the stack, then replace 0 with $\epsilon$. In other words, just pop 0 off the stack.
Language of Pushdown Automata
Accept by Final State
Accept by Empty Stack
Equivalence of PDA and Context Free Language
Lemma 1 approach
Lemma 2 approach
Achieving Chompsky Normal Form (CNF) - for CFL's
Consists of three steps:
- Clean-up of the grammar
- Eliminate $\epsilon$-productions
- Obtain list of nullable symbols n(G). A is nullable if $A^* \Rightarrow \epsilon$
- Obtain new grammar rules that are all combinations of existing rules, but without epsilon values
See March 18 notes and week 07 slides pg 4. Basically go through all combinations of rules and 'exercise' the epsilons. Below is an example.

- Eliminate Unit Productions
- Make a list of all unit productions, starting with basis (A, A)
- Extend the list with inductive case: given unit (A, B), if B has a Unit Rule that points at C, like $B \rightarrow C$, then add the unit (A, C)
- Make a table of Unit Pairs and final rules: for ea Unit Pair (A, B), have any rules that DO NOT involve units. Ie, no single Variables. Multiple variables or Terminals are fine
- Eliminate Useless Symbols
- Remove all non-generating symbols & all production rules involving 1 or more non-generating symbol
- Eliminate non-reachable symbols
- Eliminate $\epsilon$-productions
- For bodies of length ≥ 2, no terminals allowed
- Break bodies of length ≥ 3 into a cascade of 2-variable bodied productions
Pumping Lemma for CFL
Similar to the pumping lemma for Regular Languages, this is used to prove that a particular language is *not* context-free. The form is just a little different
Turing Machines
- Any algorithm that is computable can be implemented using a TM. (and vice versa)
- A language is decidable if a turing machine accepts it. An undecidable language may cause the TM to look for a solution forever
- Any programming language with an "if" conditional statement is turing-complete
Instantaneous Description
Example: $q_00011 \vdash Xq_1011$ This has the TM initially in state $q_0$ with a 0 ready to be consumed from the tape. The 0 is consumed and the head moves to the right on the tape after replacing that 0 with an X, and the state transitions to $q_1$.
Next-Move Function
$(q_1, X, R)$ - this function transitions to state $q_1%, replaces the input symbol with an X, and moves the head to the right on the tape
The Halting Problem (HP)
Given a description of an arbitrary computer program, decide whether the program finishes running or continues to run forever
This is an example of an undecidable problem.
Recognizability & Decidability
Undecidable: a decision problem where it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer
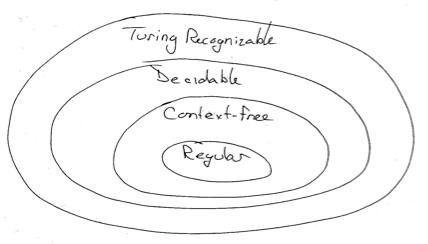
Summarizing Venn Diagram of Grammars