Sampling is the division of the domain, while quantization is the division of the range

Some general matlab functions and code

					% show the image with pixel info
					imshow('moon.tif'), impixelinfo 
					% reads the image into image1 variable	
					image1=imread('moon.tif'); 
					% shows all the variables
					whos 
					% displays 2 images in a figure
					figure, subplot(1,2,1), imshow(image1), 
						subplot(1,2,2), imshow(image2)
					% for following subplot...
					% m = # of rows
					% n = # of columns
					% p = position where the image will go  
					subplot(m,n,p)

						% creates an image, imgDbl that uses 
						% 8 bytes per pixel
						f = double(imageUint8) 
						% converts to a matrix of doubles between 
						% 0 and 1
						f2 = im2double(f) 
						imwrite(f2, 'myPicture.jpg', 'quality', 50)
						[rows, cols] = size(f2)
						
						%loop through specific values:
						someVals = [1 3 4 6 10]
						for k = 1:length(someVals)
							theVal = someVals(k)

An image transformation function, in general, is some function that is used to adjust the intensity values of the pixels in an image. Depending on the function, all or only some of the pixels will be adjusted. These functions are used for applications such as contrast improvement.

Histogram Equalization

The purpose is to correct a poor image pixel intensity histogram. The ideal histogram shape is a flat line that evenly covers all intensity values. This would imply that every intensity is used equally among all the pixels. As opposed to a histogram that is narrow (bunched in one region) - this indicates that all the pixels use only a small subset of the possible intensity values. This means the contrast is poor.

Histogram Matching

Matlab can attempt to adjust the image pixel intensity histogram and match it with a histogram provided by the user.

Matlab

					g = histeq(f, hgram)
					hgram = (hgram(1), hgram(2), ..., hgram(256))
					% Useful histogram shape: gauss curve: 
					% 	$g(x) = A \cdot e^{\frac{-(x-m)^2}{\sigma^2}}$
					% example of generating a gauss-based histogram
					x = linspace(0,1,256); 	% evenly spaced array 
					m = 1/2; s = 0.1; 		% params for gauss
					y = exp(-((x-m)/s).^2); %gauss fmla
					% scale down so the sum of everything is 1
					y = y / sum(y);

Histogram curve in above code: $g(x) = A \cdot e^{\frac{-(x-m)^2}{\sigma^2}}$

Transformations result in pixels being relocated, and often the boundaries of the image matrix changing

Affine/Projective

An affine transformation results in an image that is scaled, mirrored, translated, or skewed (maybe more). Projective transformations provide a change in apparent depth of some portion of the image. They both use a matrix in the form: $\begin{pmatrix} a & b & e \\ c & d & f \\ b_1 & b_2 & 1 \end{pmatrix}$

Where a = x scaling, b = y shearing, c = x shearing, d = y scaling, b1 & b2 offer translation, and e & f are used for projection, but set to 0 for non-projection affine

Rotation

Rotation (clockwise) uses an affine transformation matrix in the following form: $\begin{pmatrix} cos\Theta & sin\Theta & 0 \\ -sin\Theta & cos\Theta & 0 \\ 0 & 0 & 1\end{pmatrix}$

Aside: Interpolation

In transforming images, resultant calculated pixel locations are not always exact integers, but they need to be coerced into integer locations using some form of interpolation. There are three main ones, from simplest to most complex: Nearest neighbour, Bilinear, Cubic Polynomial. The default in Matblab is Bilinear, but nearest neighbour may work better in many cases.

Matlab

					% here T is a standard matrix in a form mentioned above
					tform = maketform('affine', T [, 'FillValue', alpha])
					% FillValue with alpha is optional, but fills any empty 
					% space created at the edge of the matrix with some intensity value give by $\alpha$
					g = imtransform(f, tform)

Point-based Registration

Image Registration is the transformation of a given image to conform in some way to a base image. Control points are selected on the base image, then the input image is transformed in a way that the same points are found on as those selected on the base image, and they points are moved to be in the same position as the base image. Used in applications where the subject of the image needs to be in a consistent location in the frame.

Matlab

					% this brings up a nice interface for selecting points then use file->export points to workspace
					cpselect(input_img, base_img)
					% for TransformationTypes  Affince and Projective...
					% P = input control points, Q = base image control points
					tform = cp2tform(P, Q, 'TransformationType')
					% imtransform can return x and y coords info which is useful
					% for plotting.Then use impixelinfo to find where to crop
					[ f1, xdata, ydata ] = imtransform(f, tform)	
					% how to plot orig and translated together	
					imshow(f, 'XData', xdata, 'YData', ydata);hold on;
					imshow(f1);axis on;axis auto;

Area-based Registration

Here we choose a template, which is a section of an image, that is used to compare against another image to see if there is a matching section. The matching process is called normalized cross-correlation.

					% we can choose a template from an existing image, like g. This just graphs a square of image g.
					template = g(10:20, 10:20)
					% the template is then used for cross-correlation against one of the images.  The max value(s) 
					% indicate the highest correlation (probably a match)
					g = normxcorr2(template, f)
					dx = ... % find diff between x in one img and t'other
					dy = ... % find diff between y in one img and t'other
					tform = maketform('Affine', [1 0  0; 0 1 0; dx dy 1]);
					% yadda		

Determine various properties of a image. Often used in identifying or counting objects in an image. The image must be turned in a "boolean" image (basically B&W) so regions can be recognized. Thresholding is used to convert to boolean.

Thresholding

Here we must choose a threshold, $t$, for converting

$g(x,y) = \begin{cases} 0 & if\ f(x,y) \leq t \\ 1 & if\ f(x,y) \gt t \end{cases}$

Then g = f > t.

Erosion (thining) $A \ominus n B$

For a given structuring element (often a square matrix), the image area is reduced in size given the logical rule that the entire structuring element must be a subset of the area in question. We can repeat this process n-many times (where n is ≥ 1, but usually is just 1).

Dilation (thickening) $A \oplus n B$

For a given structuring element, the image area is increased in size given the logical rule that the area can be made to occupy any area such that the any part of the structuring element intersects the original area. Img below shown with two square structuring elements. We can repeat this process n-many times (where n is ≥ 1, but usually is just 1).

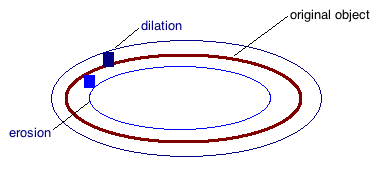
Matlab

					% where 'a' is a binary img, and 'b' is a structuring element
					c = imerode(a, b)
					% or...
					c = imdilate(a, b)
					% and to create an SE: 
					b = strel('Square', 3) % creates a 3x3 square structuring el

					c = imopen(A,B)

					c = imclose(A,B)

						gFilled = imfill(g_swissCheese, 'holes')

				function xnew = findComponent( i, j, f )
				    xnew = zeros(size(f));
				    xold = xnew;
				    xnew(i,j) = 1;
				    b = [ 0 1 0; 1 1 1; 0 1 0 ];
				    while any(xold(:) ~= xnew(:))
				        xold = xnew;
				        xnew = imdilate(xnew, b) & f;
				    end
				end

Morphological Reconstruction

This allows us to reconstruct components of an image that were possibly removed during intensive erosion. Same algorithm as component finding except initial point $X_0$ is a set, or matrix, of points.

Typical way to find F: erosion of the original image $A \ominus n B$

Matlab:

					imreconstruct(F, A, Connectedness) % Connectedness is 4 or 8

Greyscale Morphology

The following tools are useful in greyscale morphology before thresholding

Dividing up an image into distinct regions based on some criteria, like qualities of edges or regions. Additional techniques often need to be employed such as pre-segmentation sharpening (and pre-segmentation-sharpening blurring).

Edge-based segmentation

In the following matlab sample, the extra 't' output parameter is matlab's attempt at finding a reasonable threshold if you do not provide the optional T input parameter. You can use this output param as a guide for choosing your own appropriate input T parameter

		[ g, t ] = edge(f, method, T)
		[ g, t ] = edge(f, 'log', T, sigma)
		[ g, t ] = edge(f, 'canny', [Tlow, Thi], sigma)

Region Based Segmentation

Region-based segmentation (by inspection)

With region-based segmentation, we segement the image based on a threshold obtained by the intensity of particular regions. The approach essentially boils down to using a histogram. Depending on the image, the threshold can be ascertained simply by inspecting it (in the case of two distinct humps), or by using a more complex algorithm like Otsus. For an image with a histogram like the one below, we can simply choose the threshold by inspecting the historgram and choosing the low point between the humps.

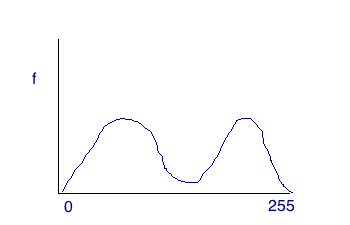
Region-based segement with Otsus

For image histograms that lack the distinction between two regions, we need to use a more powerful technique. The Otsus method uses a statistical algorithm to find the optimal threshold. This will work for both simple and relatively complicated histograms. The red line in the image below is the actual histogram, while the blue humps are the "hidden" truly distinct regions. Otsus can uncover the distinct humps (in most cases).

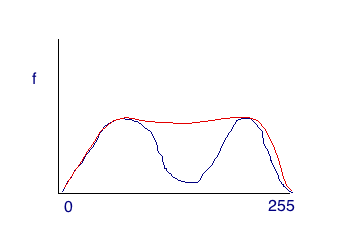
		%Otsus is graythresh (returns value from 0 to 1)
		T = graythresh(f)
		g = f > T*256.

Three-Region Segmentation

For segmenting into three regions, if possible, just look at the histogram. If the histogram does not have the necessary three distinct humps, then blurring is one option.